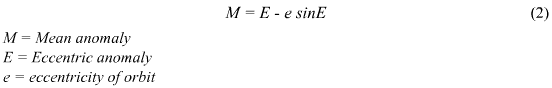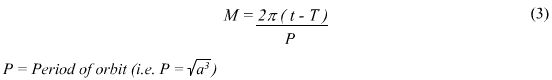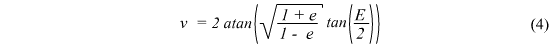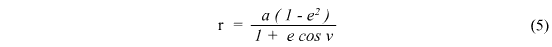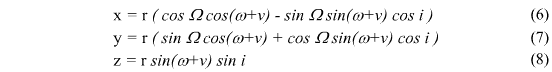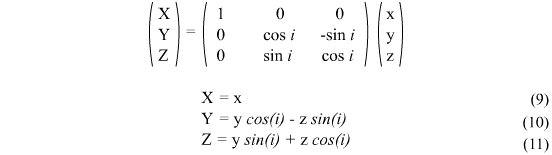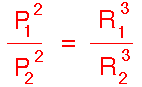Blog Week 3 - Orbital Elements and Project Spec

This weeks blog will be relatively short, as I will also be writing a Project Specification, which is due in a week today. Here is an overview of what it will contain:

•   The project specification is a more detailed description of the work to be done. Two sides of A4 should suffice. 
• This should document the initial avenue of research / development which the student follows; indicate any prototype developments which are envisaged; suggest comparative studies of different design approaches etc. The initial project plan should be drawn up after a preliminary investigation of the literature. 
• This deliverable is not formally marked, but it will inform the supervisor’s assessment of conduct. Failure to submit on time (without good reason) will have a negative effect on the conduct grade.

Following my supervisor meeting this week, it became clear that I was looking in the wrong area for the equations I needed to calculate an orbit. What I needed were Orbital Elements. These are 6 elements, some detailed in the diagram below, from this website. 

 

The actual 6 orbital elements are:

Eccentricity (e)
Semimajor Axis (a)
Inclination (i)
Longitude of the ascending node (Ω)
Argument of periapsis ()
Mean anomaly (M)

First, a couple of equations are needed to calculate the planets polar coordinates, (r, v). Kepler's equation allows us to solve the Eccentric anomaly, once we have calculated the Mean anomaly. The two equations are shown below:

 

Once E has been calculated, r and v can be:

I can make use of this data to calculate the Heliocentric Ecliptic coordinates (x,y,z) for a planet, which are an X,Y,Z coordinate system centered on the Sun in which the ecliptic lies in the X-Y plane. The equations to calculate these points are:

Now, what I really need are the Heliocentric Equatorial coordinates (X,Y,Z) for a planet, in which the coordinate system centred on the Sun with the Sun's equator lying on the X-Y plane - the type I will base my system around. The equations to calculate these points are:

 

Onto the most important part of the blog - this data is confirmed in a PDF document on the JPL Solar System Dynamics website (a NASA source). The PDF also lists the Keplerian Elements for the time period 1800 AD - 2050 AD, an invaluable resource for me to be able to calculate the planetary orbits for this project. It should be noted that the website states that the data for these positions is only approximate, but it should be efficient enough for this project.

Blog Week 2 - Orbits

This week I'm focusing on finding out more information about planetary orbits. Firstly I'd like to recap on some of the thoughts in the previous blog following this weeks meeting with Rob Lothian (my project supervisor);

• Planetary bodies - due to the complex nature of getting the actual planets to orbit, creating different orbits for moons may be too much for this project. I think I'd like to include moons - at the very least for the Earth - but this is something that will need to be considered later in the project.
• A third scale may be required for the Sun (the first being distance between the planets, and the second the size of the planets in relation to each other). This is however something that can be looked at and played around with once the basic orbital coding is done.
• Selecting a starting date for the program will just be done using accurate data, not using any "planetary alignments", so to speak.

Now, on to this weeks work. Following the honours project talk we had midweek, I've starting producing a Mind Map. Hopefully mainting this and the blog will prove extremely useful when it comes to writing up the final report for this project.

For this weeks research on orbits, I have been using a variety of websites - applet-magic states that a planets orbit is calculated by the balance between the gravitational attraction between the planet and the Sun, and the centrefugal force from it's movement in a approximately circular orbit.
The site details that in order to calculate a planets orbit, five main points - called Lagrangian points - are needed. It goes on to explain the math behind this, although it doesn't appear to be finished. To be honest, the math goes right over my head, and it's very difficult to understand.
On the same website - http://www.applet-magic.com/orbital.htm - they have a table of orbital velocities which also includes information on the length of a year and the orbital radii of the planets, in relation to the Earth.

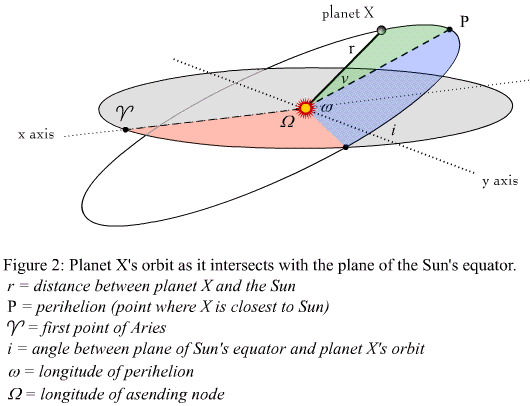
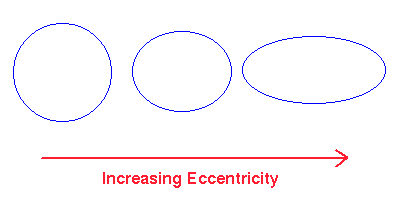
One important point to note about orbits is that they are not circular, they are elliptical, and each planet has an eccentricity value between 0 and 1 - the close to 0, the more circular the orbit, the closer to 1, the more flat.

I found a useful table documenting these values for 6 of the 8 planets:

Planet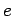
Mercury	0.206
Venus	0.007
Earth	0.017
Mars	0.093
Jupiter	0.048
Saturn	0.056

Upon further study, perhaps a better way to calculate the orbit of the planets would be to use Kepler's Law's of Planetary Motion. These are (from istp.gsfc website):

1. Planets move around the Sun in ellipses, with the Sun at one focus
2. The line connecting the Sun to a planet sweeps equal areas in equal times.
3. The square of the orbital period of a planet is proportional to the cube (3rd power) of the mean distance from the Sun (or in other words--of the"semi-major axis" of the ellipse, half the sum of smallest and greatest distance from the Sun). Shown below (from this website):

The astro-tom website explains how Kepler's third law can be used to calculate the orbits of other planets, given certain data. The equation used is;

P (years)² = R (A.U.s)³

Where P is the period of the planets (measured in Earth years), and R is the length of the semi major axis of the planet's orbit (measured in an astronomical unit, the average seperation of the Earth from the Sun).
The website demonstrates how the semi-major axis length of Mars can be calculated given it's orbital period.

On the istp.gsfc website, an alternate equation is given:

r = a(1 – e²)/(1 + e cos f)

 

Where a is the length of the planet's semi major axis, e is the eccentricity value and the polar coordinates are (r,f).

Overall, I'm pretty confused about which equations I should be using, and even how to implement them, so this is definately something I will need to discuss with Rob.

Interesting links

http://dunnbypaul.net/ssdisckit/ -  a complex digital orrery. Contains useful references.

http://cfa165.harvard.edu/software/catalogs/sao.html - Star catalog, lots of information on many stars.

http://www.exploratorium.edu/ronh/solar_system/ - Scaling calculator - calculates planet sizes and orbits given a scaled size of Sun. Contains a link to given scaled sizes of moons and various other satellites too.

http://www.burtleburtle.net/bob/physics/solar.html#ref - small digital orrery, lots of useful references

Planet Textures

Whilst researching orbits this week, I also stumbled across some great websites which contain free to use textures of all the planets, and in some cases a few moons also. These resources will be incredibly useful for the planets aesthetics when it comes to modelling the planets in 3Ds Max. I've published this as a seperate blog so it's easier to find when the time comes for me to do the modelling.

http://planetpixelemporium.com/ - texture maps for all the planets and some moons, 1k versions for free. Also contains some tutorials.

http://www.mmedia.is/~bjj/planetary_maps.html - lots of texture maps, plus detailed information about each map.

http://maps.jpl.nasa.gov/ - database of texture maps, including some of high quality available for free.

Blog Week 1 - Direction

The first decision that I need to make in undertaking this project is which direction I would like to take the project in.

The coding language I have settled on is C++. Programming in this language means I can interact with OpenGL far easier than I could in other languages, such as Java. The orrery program should allow the user to view the planets orbiting the Sun initially from the furthest point out, with the option to zoom and view the other planets. Intial timescale should relate to a day passing every second, but the user will have the option to increase this in order to see the planets orbit at a higher speed. 

I am unsure yet as to how many moons I will include in this program. Initially I had thought to include only moons with a radius greater than 1000km - this gives me 16 planetary bodies in the system:

• The Sun
• Mercury
• Venus
• The Earth
• The Moon 
•  Mars
• Jupiter
• Io
• Europa
• Ganymede
• Callisto
• Saturn
• Titan
• Uranus
• Neptune
• Triton

This means that none of Mars' or Uranus' moons and only one of Saturn's and Neptune's would be included. This is something I will need to discuss further with my supervisor before making a cast iron decision. I do not think that the dwarf planets (such as Pluto) will be included, but as I say this is something I need to discuss and return to.


The following is a list of programs that I intend to use during this project:

• Microsoft Visual Studio 2010 - for C++ programming
• Autodesk 3Ds Max 2011 - for modelling of planets etc
• Microsoft Word 2010 - any necessary word processing
• Adobe Photoshop CS5 - texture editing etc

I will be using this blog to keep track of any links with useful information that I feel may prove useful in the future of the project. Here are a few that I have come across during my intial research this week:

http://nineplanets.org/ - comprehensive information site on the eight planets (despite the name), their moon, dwarf planets, and various other small bodies in the solar system.


http://star.arm.ac.uk/~dja/planets.html - orbital positions of the planets, dating from January 2000 to projected positons in December 2019.

http://www.etsu.edu/physics/etsuobs/starprty/22099dgl/planalign.htm - information on Planetary aligments. I had initially thought that a "planetary alignment" would make a perfect starting time for the program, yet this seems more complex than I had first realised.

http://www.easytorecall.co.uk/orrery_simulation.htm - A very basic Javascript 2D digital orrery. Shows orbits of Mercury, Venus, Earth and Mars and their moons around the Sun.

http://www.gifford.co.uk/~principia/orrery.htm - Another very simple digital orrery. Shows all planetary orbits, but no moons. Also shows current position of planets.

Welcome

Welcome to my honours project blog.

This blog should contain weekly updates, detailing what I've worked on in the current week. I'll also post any links to interesting information or good websites that I've used to aid my development of this project.

The project I have chosen to do is to produce a digital orrery. An orrery is a mechanical device which demonstrates the planetary postions (with their moons) and orbits in the the solar system, an example is below:

 
My task is to reproduce this in a digital form on a computer.

Update on this weeks work coming up!